文|新智元

编辑|肖琴 鹏飞

刘慈欣的科幻小说《三体》描述了一个地外文明，被称作”三体人“。三体人所在的行星受到3颗相互制约的恒星影响，导致该文明一直处于水火两重天的极端天气中，而这群顽强的三体人也在为了精确计算这三颗恒星的轨迹而挣扎。

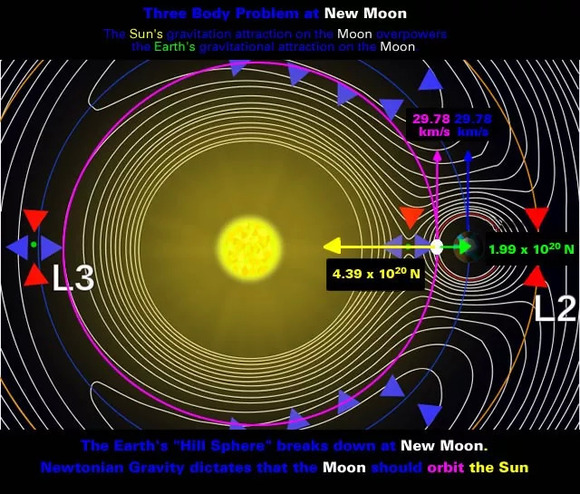
实际上，“三体问题”从几百年前开始，就是一直困扰数学家的难题。三体问题是多体问题中的一例。多体指的是多个相互作用的实体，例如二体指的是两个实体、三体指的是三个实体。传统上说的三体就是太阳、月亮以及地球。

二体问题早在牛顿时期就已经被完美解决了，但是目前物理学中任何三体问题，都没有一个“闭合”形式的解析解。

当然这并非意味着这是个“无解”问题，只不过求解过程需要近似和数值技术来进行计算，同时还需要足够精确的数值来计算分析三体之间的关系。而我们目前使用的分析方法的局限性，无法满足上述的精度需求。

如今，随着人工智能的发展，研究人员发现深度神经网络在解决“三体问题”方面，能够起到惊人的提速作用！爱丁堡大学、剑桥大学等发表在arxiv的一篇论文《Newton vs the machine: solving the chaotic three-body problem using deep neural networks》中表明，训练人工神经网络能在固定计算成本内提供准确的解，速度提升了1亿倍！

什么是三体问题？

18世纪的科学家面临一项巨大的挑战：如何在空旷无垠、缺乏位置参考系的海面上，对船只实现精确定位？

最终，科学家利用恒星（也就是太阳）当做一个固定的坐标，利用太阳、月亮、地球之间的引力关系，在一定程度上解决了这个问题，这就是三体问题最简单的例子。

三体问题是天体力学中的基本力学模型，最早可以追溯到1687年，由牛顿在《自然原理》中提出：定义和研究三个大质量物体在相互吸引的引力作用下的运动问题。

如今，广义的三体问题指的是研究三个可视为质点的天体，在相互之间万有引力作用下的运动规律问题，也就是不仅仅局限于太阳、月亮、地球，可以是任何受引力相互作用的物体，它们的质量、初始位置和初始速度同样都是任意的。

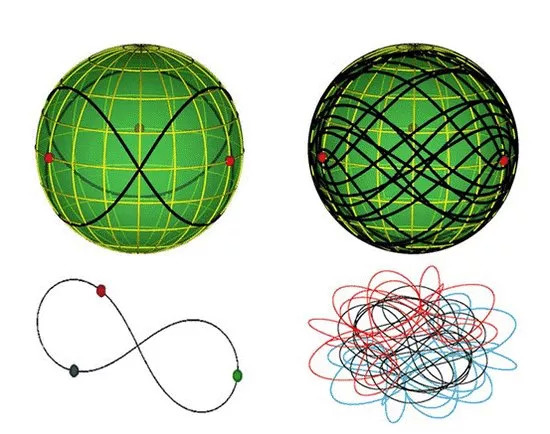
根据维基百科，在三体问题的解决过程中，法国数学家庞加莱做出了巨大的贡献，提出了限制性三体问题：即三体中其中两体的质量极大，以至于第三体的质量完全不能对其造成任何扰动。面对这个问题，庞加莱运用了他发明的相图理论，并且最终发现了混沌理论。

庞加莱发现这个系统的演变经常是混沌的：如果初始状态有一个小的扰动，例如一个体的初始位置有一个小的变动，则后来的状态可能会有极大的不同。如果该小变动不能被我们的测量仪器所探测，则我们不能预测最终状态为何。

这就是为什么我们说三体问题在一定程度上被解决，而并非彻底被解决。现在已知，三体问题还无法被精确求解，即无法预测所有三体问题的数学情景，只有几种特殊情况可以研究。

为什么三体问题一直无法被精确求解？

“在研究多体问题时，问题的复杂程度会随着个体的增多成指数级增长，想把这些作用全部考虑在内简直是不可能的”，德国加尔兴的马克思·普朗克量子光学研究所的物理学家马瑞-卡蒙·巴纳尔斯（Mari-Carmen Ba?uls）说道。

根据东南大学甘庆雨论文，在一般三体问题中，每一个天体在其他两个天体的万有引力作用下的运动方程都可以表示成 3 个二阶的常微分方程，或 6 个一阶的常微分方程。

因此，一般三体问题的运动方程为十八阶方程，必须得到 18 个积分才能得到完全解。

虽然从理论上可以证明三体问题属于决定论问题，但要想得到通解表达式，通过降维的方法意味着我们需要 18 个不变量条件，然而目前只有 10 个（质心方程 3 个，动量守恒方程 3 个，角动量守恒方程 3 个，能量守恒方程 1 个），所以说在解析上还远远解决不了三体问题。

而目前所采用的一般方法是规则化，比如假设轨道是规则的椭圆形、且处在同一个平面内，或者假设已知三体中的1个天体质量相对可以忽略（例如太阳、月亮、地球中的月亮），将三体问题转化为二体问题来处理。然后对精度进行修正，直到精度满足所需条件为止。因此，迫切需要一种新的，更强大的方法来解决三体问题。

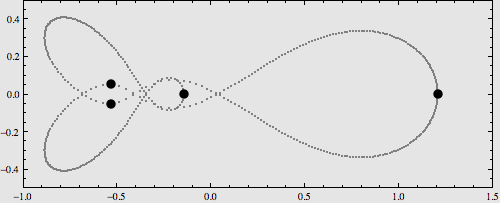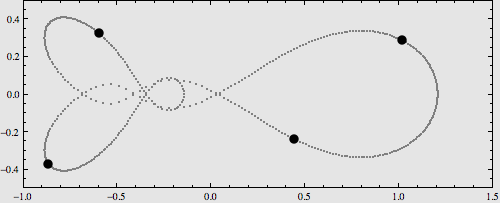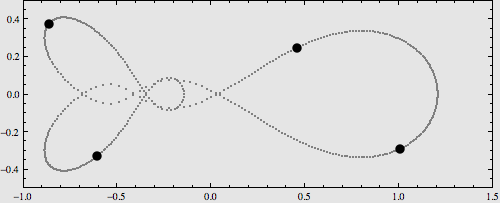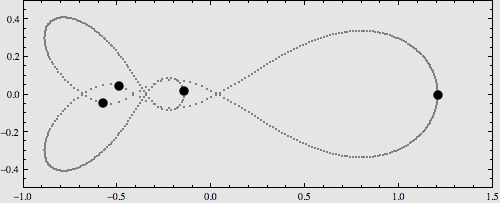
四体问题的特殊解

神经网络成为突破关键！

神经网络似乎成为一个非常不错的选择。早在2017年，Johannes Kepler 大学、DeepMind、OpenAI 和 Facebook 纷纷发表论文，探讨了使用深度神经网络来解决多体问题。

LSTM 之父Sepp Hochreiter就提出利用模拟库仑力（即电磁力大小与反向距离的平方成比例）作为一种训练生成对抗网络（GAN）的替代目标函数。

近日，爱丁堡大学的Philip Breen等训练神经网络来计算三体问题方程，该网络以固定的计算成本提供了准确的解决方案，比最先进的传统求解器快了1亿倍！

神经网络解决三体问题，速度提升1亿倍！

神经网络似乎成为一个非常不错的选择。早在2017年，Johannes Kepler 大学、DeepMind、OpenAI 和 Facebook 纷纷发表论文，探讨了使用深度神经网络来解决多体问题。

LSTM 之父Sepp Hochreiter就提出利用模拟库仑力（即电磁力大小与反向距离的平方成比例）作为一种训练生成对抗网络（GAN）的替代目标函数。

近日，爱丁堡大学的Philip Breen等训练神经网络来计算三体问题方程，该网络以固定的计算成本提供了准确的解决方案，比最先进的传统求解器快了1亿倍！

作者表明，训练人工神经网络(ANN)来执行这些计算，能以固定的计算成本提供精确的解，而且比最先进的传统求解器快 1 亿倍！

该结果提供了证据，即对于在相空间上具有计算挑战性的区域，计算挑战相空间的区域，一个训练好的人工神经网络可以代替现有的数值求解器，从而能够快速、可扩展地模拟多体系统，以阐明诸如黑洞双星系统的形成或密集恒星团中核塌缩的起源等现象。

来自爱丁堡大学、剑桥大学等的研究人员在论文“Newton vs the machine: solving the chaotic three-body problem using deep neural networks”中详解了他们的方法。

每个人工神经网络都需要一个学习阶段，在这个阶段中，自适应模型的参数将使用一个训练数据集进行调优，这使得预测精度对于训练集是否代表未来数据应用中可能出现的模式类型非常敏感。因此，针对混沌问题训练ANN要求跨各种初始化提供一组解。获得这样一个训练集的唯一方法是对一个大而多样的实现范围内的运动方程进行数值积分，直到获得一个收敛解为止。

Breen 和他的同事们首先简化了这个问题，把它限制为三个质量相等、初始速度为零的粒子在一个平面上的引力问题。他们随机选择起始位置，并用最先进的 Brutus 法求解它们的三体运动。然后重复这个过程 10000 次。

图1：初始粒子的位置

训练和验证数据集分别由9900和100个模拟组成。在每个模拟中，随机生成粒子的初始位置，并计算轨迹，使用Brutus对运动方程进行积分。生成这些数据需要超过10天的计算机时间。

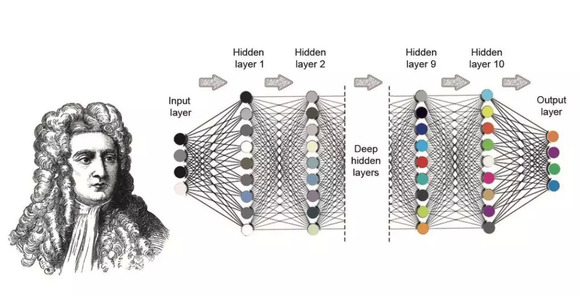
图2：牛顿和神经网络

研究人员使用包含10个隐藏层、128个互连节点的前馈神经网络，如图2所示。通过将时间t和粒子x 的初始位置输入到输入层中，神经网络会在时间t返回粒子x 和x 的位置，从而近似解决一般三体问题的潜在解析解。

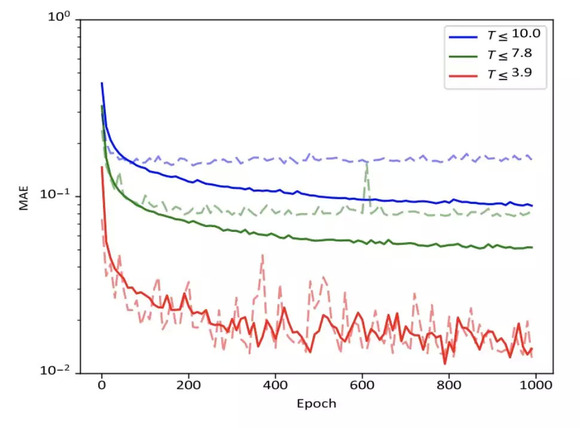
图3：Mean Absolute Error (MAE) vs epoch

表现最好的人工神经网络是t<3.9，如图3所示。

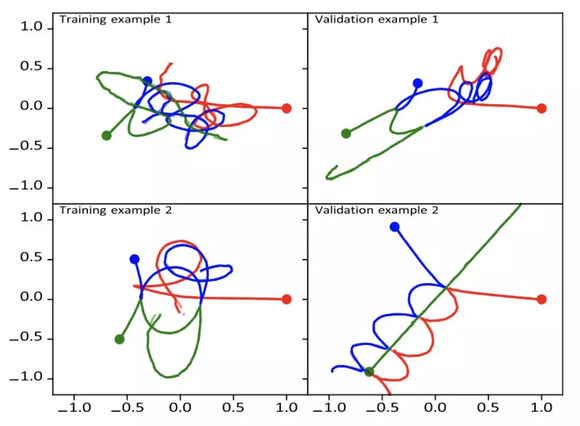
图4：训练后的人工神经网络的有效性

图4给出了基于该ANN对训练集(图4，左)或验证集(图4，右)内收敛解的预测示例。在每个场景中，粒子轨迹反映了一系列复杂的相互作用，经过训练的人工神经网络令人满意地再现了这些相互作用(MAE≤0.1)。人工神经网络还与所有未纳入其训练的情形下收敛解的复杂行为密切相关。

此外，ANN在固定的计算时间(t～10 3秒)内完成了计算，平均大约比Brutus快10 倍(有时甚至是10 倍)。

研究人员表示，随着成功准确地再现了一个混沌系统的结果，他们感到鼓舞的是，其他类似复杂性的问题也可以通过训练机器学习算法来取代经典的微分求解器来有效解决。

研究人员表示下一步是扩大动态范围，放宽一些关于对称性和质量的假设，从而构建一个网络来解决一般的三体问题。

他们设想，这个网络可以解决更复杂的混沌问题，比如4体和5体问题，从而进一步减少计算负担。

该研究的意义是什么？

作者声称已经证明深度的ANN可以在固定的时间间隔内，为三体问题提供快速而准确的解决方案。

尽管研究人员的初始设置得到了简化，但粒子轨迹仍会定期进行一系列复杂的交互作用，而ANN会捕获这种行为，从而以任意的计算时间成本来匹配任意精确的数值积分，从而得到的预测。

传统积分器无法在预定时间容限内计算数值解的相空间区域，而训练有素的ANN则可以用来提供对远离当前计算困难区域的粒子位置的准确预测。然后可以将这些预测用作输入变量，以在将来某个时间点重新启动传统积分器。

该方法将传统积分器与ANN相结合，从而获得比目前可实现的场景更加广泛精确及时的三体问题解。

研究人员已经证明，在考虑的参数空间内，ANN有助于对大型系统进行更易处理和可扩展的评估。

随着研究人员成功、准确的再现了混沌系统的结果，研究人员受到鼓舞的是：可以通过在基础物理过程训练的机器学习算法，来代替经典的微分求解器，从而有效地解决其他类似复杂性问题。

研究人员的下一步是扩大动态范围，放宽一些关于对称性和质量的假设，以构建可以解决一般三体问题的网络。

最终，研究人员设想可以对网络进行更丰富的混沌问题的训练，例如四体和wu't体问题，从而进一步减轻计算负担。

参考来源：ArXiv