文|新智元

编辑|金磊 小芹

超级大整数相乘极限速度实现了！

整数相乘是每个人必学的一个运算，我们通常采用的思路是：第一个数字的n位乘以第二个数字的n位，这就意味着要进行n2次的乘法运算。但当这两个整数大到一定程度时，这个过程的计算量是相当庞大且惊人的。

当然，前人们已经找到了一些解决方法来改善这一问题。早在1971年，两位德国数学家就猜测，两个大数相乘的可以达到一种令人难以置信的速度，即N log (N)。然而，这个聪明的想法几十年来一直只是假设。

直到现在，这个假设终于被证明了！

澳大利亚新南威尔士大学(UNSW)的数学家、副教授David Harvey近日声称，他和他的合著者首次破解了这个由Arnold Sch nhage 和 Volker Strassen提出，存在近半个世纪之久的数学难题。

论文地址：

 

简单来说，这项研究采用了1,729维快速傅里叶变换(FFT)，使得计算速度达到了N log (N)——目前理论上的极限值。

以前，两个十亿位的整数相乘，若是采用常规算法，大约需要几个月才能算出它们的结果。但是应用该新算法，仅需30秒！

数学处处充满惊喜，大数乘法速度屡破记录，或已至极限

两个整数相乘很简单对吧？

小学的时候我们就学过如何做整数的乘法运算，例如：

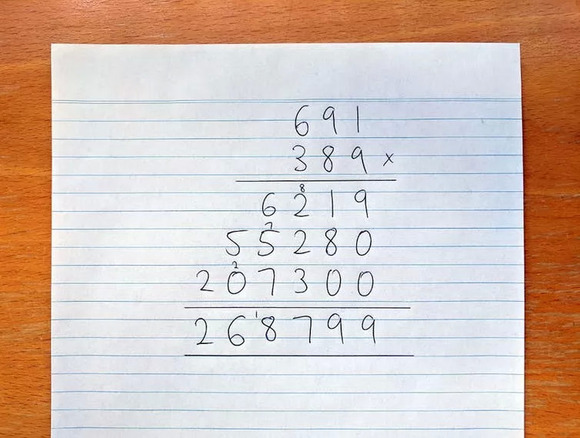
但是，若是整数长度大到了一定程度，这种方法真的是最好的吗？

在一般的乘法运算过程中，我们需要把第一个整数的每一位和第二个整数的每一位做乘法。如果这两个数都有N位，那就是N2(或N x N)相乘。在上面的例子中，N是3，所以我们要做32 = 9次乘法。

1956年前后，著名的苏联数学家安德烈·科尔莫戈罗夫(Andrey Kolmogorov)推测，这就是两个整数相乘的最好方法。

换句话说，不管你怎么安排计算，你要做的功至少与N2成正比。两倍的数字意味着四倍的工作量。

科尔莫戈罗夫认为，如果有更简便的方法，那肯定已经人们发现了，毕竟人类在“乘法”这件事儿上探索了千年之久。

被打脸，更快的方法诞生

然而，就在几年后，科尔莫戈罗夫就被打脸了。

1960年，23岁的俄罗斯数学系学生阿纳托利·卡拉苏巴(Anatoly Karatsuba)发现了一种代数技巧，可以减少所需的乘法次数。

例如，要乘四位数的数，不需要42 = 16的乘法，卡拉苏巴的方法只需要9次。当使用他的方法时，两倍的数字只意味着三倍的工作量。

而且随着数字位数的增大，这种方法的有效性越发显著，对于一千位数字的相乘，比之前的方法所需的乘法次数要少17倍。

大数字相乘在生活中的应用

有人会很好奇，谁会用到这么大的数字来做乘法呢？事实上，现实生活中由大量的应用是需要这么做的，最典型的就是密码学。

每次我们在互联网上进行加密通信时（例如，访问银行网站或执行网络搜索），我们的设备都会执行的乘法次数是非常恐怖的，涉及数百甚至数千位的数字。

对于一些更深奥的应用程序，数学家必须处理更大的数字，数百万、数十亿甚至数万亿的数字。对于如此庞大的数字，即使是卡拉苏巴的算法也是太慢了。

1971年，德国数学家阿诺德·绍哈格(Arnold Schonhage)和沃尔克·斯特拉森(Volker Strassen)的工作取得了真正的突破。他们解释了如何使用快速傅里叶变换(FFT)来有效地对“大数字”做乘法。今天的数学家经常使用他们的方法来处理数十亿位数的数字。

极限速度猜测

在他们1971年发表的论文中，他们也提到了一个惊人的猜测。

他们猜测的前半部分是，应该有可能使用最多与N log (N) (N乘以N的自然对数)成比例的一些基本运算来乘N位数字。但他们的算法并没有达到这个理想的结果，速度慢了一个log因子(log N)。

而后的研究者们对此进行了不懈的深入挖掘，但直到2007年，Martin Furer的工作也只是接近N log (N)。

猜测的后半部分是，N log (N)应该就是速度的极限——没有任何可能的乘法算法能做得比这个更好。

乘法运算速度极限已经实现？

就在前几周，Joris van der Hoeven和David Harvey共同发表的一篇论文《Integer multiplication in time O(n log n)》描述了一种新的乘法算法，最终达到了N log(N)这一“圣杯”。

该算法突破性重点在于使用多维FFT，而不是仅仅使用一维FFT。自1971年以来，在很多领域都会涉及多维FFT的应用，例如JPEG格式图像依赖于二维FFT，而三维FFT在物理和工程中有很多应用。

而在这篇论文中，所用到的FFT维度高达1,729。

但是，以目前的形式来看，新算法实际上并不实用，因为论文中给出的证明只适用于非常大的数字。即使每个数字都写在氢原子上，在可观测的宇宙中也几乎没有足够的空间把它们写下来。

另一方面，作者还希望通过进一步的改进，使得该算法可以应用于只有数十亿或数万亿位数的数字。如果是这样，它很可能成为计算数学家“军火库”中不可或缺的工具。

若Schonhage-Strassen猜想是正确的，那么从理论的角度来看，新算法就是这条路的终点——不可能做得更好。

但论文作者也表示：“若猜想被证明是错误的，我会感到非常惊讶。但我们不应该忘记科尔莫戈罗夫的遭遇。”

毕竟，数学处处充满惊喜。

作者简介

David Harvey

新南威尔士大学数学与统计学院副教授和ARC未来研究员。研究领域包括计算数论与算术几何，多项式与整数算术。

所获奖项：

2017–2021: Counting points on algebraic surfaces ($805,054)ARC Future Fellowship, FT160100219

2015–2017: Fast algorithms for zeta functions of algebraic varieties ($325,500)ARC Discovery Project, DP150101689

2012–2014: Counting solutions to equations over fields of large characteristic ($375,000)ARC Discovery Early Career Researcher Award, DE120101293

主页地址：

https://web.maths.unsw.edu.au/~davidharvey/

Joris van der Hoeven

CNRS研究主任、MAX团队组长。主要研究集中在渐近微积分和复分析的自动化，以及快速算法。

曾与Matthias Aschenbrenner合作共同出版了《渐近微分代数与变级数模型理论》一书，证明了渐近微分代数的量词消去定理。另一个主要研究课题是具有特殊函数或更一般的微分方程解的复分析和计算的自动化。一方面，这导致了一些有趣的理论问题，如可计算性、零点测试、奇点等。另一方面，需要为多精度计算开发和实现快速、可靠和数值稳定的算法。

来源：theconversation