作者：Lynn

刚刚，在德国召开的海德堡获奖者论坛演讲上，菲尔兹和阿贝尔奖双料得主迈克尔·阿蒂亚爵士在45分钟中的演讲中，用40分钟介绍了黎曼猜想，仅用五分钟，凭借1张ppt，从量子力学中的概念出发，给出了他对159年里悬而未决的黎曼猜想的证明。

对此，众说纷纭，数学界也尚未有进一步的评论给出。

通过量子力学证明

159年未解之谜得“解”

迈克尔·阿蒂亚（Michael Atiyah，1929.4.22-）， 主要研究领域为几何，被誉为当代最伟大的数学家之一。于1966年荣获菲尔兹奖，在2004年与辛格共同获得阿贝尔奖。

图 | 迈克尔·阿蒂亚

不久之前，他提前公布了此次演讲的摘要，称：“黎曼猜想是1859年提出的著名问题，至今悬而未决。我会基于冯·诺依曼（1936）、希策布鲁克（1954）和狄拉克（1928）的相关工作，给出一个使用全新方法的简洁证明。”话语一出，在数学界里引起了巨大的轰动。

今天上午，据称是他的证明论文的预印版被流出，短短五页纸的长度与黎曼实现了隔空的遥相呼应，时隔159年，时代不同，但不变的是依然简洁。

论文摘要中写道，他希望理解量子力学中的无量纲常数——精细结构常数，并将此过程中发展出来的数学方法用于理解黎曼猜想。

图 | TODD函数

在演讲中，他抛出了自己定义的Todd函数，通过常数结构的解析，并利用反证法给出了证明思路，值得赞叹的是，尽管演讲时间只有四十五分钟，他也没有忘记向给过自己启发的数学家们和物理学家们致敬。

同时，他也表示：“此次只是给出了思路，未来也还有很多事需要我们去做。”

黎曼猜想的起源

黎曼猜想的证明如此重要，不是因为它是数学史上仅有的价值“100万美元”奖金的几个难题之一，而是它的成果已经渗入几何、代数、空间物理等众多基础科学研究中，从而足以撼动密码体系、信号分析等诸多工程的基础。

图 | 波恩哈德·黎曼

但在1859年当选柏林科学院院士时，黎曼似乎对自己会带来的惊人贡献毫不自知。作为对这一崇高荣誉的回报，他提交了一篇《论小于给定数值的素数个数》的小论文，在这篇论文中，黎曼用一个简短函数描述了一个数学家长期感兴趣的话题——素数的分布问题。而这一论文就是黎曼猜想的发源地。

整篇论文只有八页长，可想而知，黎曼的文字描述和证明过程十分简洁精炼。要命的是，论文中多处出现的“证明从略”，即黎曼认为显而易见的推理过程，有些花费了后世数学家们几十年的努力才得以补全，而有些直到今天仍是空白。

但这并不能说明黎曼不严谨，毕竟事隔三百多年才被证明出来的费马大定理，其提出者费马也没有意识到他给数学界留下了个多么大的难题。在发现费马大定理时，人们发现在公式的旁边，他只留下了一句话：因为边上没有空白，所以证明就不写了。

事实证明，数学家们也确实喜欢开这样的“玩笑”，可查阅的资料表明，黎曼就更偏爱将自己的重大思考和疑问写在给父亲的信中。

黎曼猜想是什么？

正如黎曼猜想起源的论文名一般，其重大意义就是利用了复分析解读了素数分布定律。而被采用的这道大家早已熟知的函数公式，在黎曼的“点化”下，就像一道智慧之光，打通了数论和解析几何在复分析领域的通道。自此，该函数公式就被正式定义为“黎曼zeta函数”。

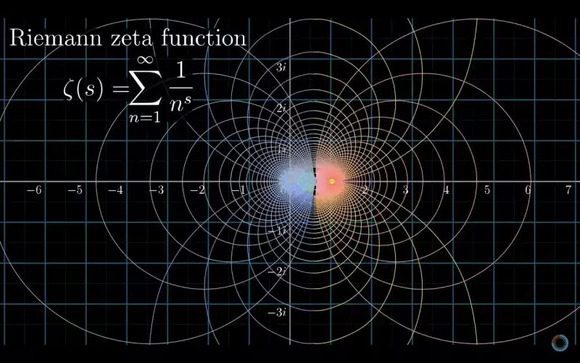
图 | 黎曼zeta函数

对于zeta函数，黎曼给出了这样的猜想：

如果

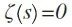
且s不是实数，那么一定存在某个实数y，使得

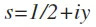
黎曼认为，这些零点有一定的排列规律，除了分布在横轴上的零点（如4，2，-2，-4，等，被称为“平凡零点”），所有的非平凡零点都集中在实部为1/2的直线上，无一例外。

基于已有的数论研究，在调整各种各样的s值时，我们会发现，ζ(s)里面合数项部分很容易就被质数项部分“吸收”了（任意合数可以分解为质数之和），而质数和质数的幂项则很难被消掉，往往会残留下来。

而对于某些s，ζ(s)居然等于0，也就意味着质数都消解光了。这就说明质数里面必然存在某种针对这个s的结构，而这就是一直被数学家们猜测探讨的质数分布规律。

不难意识到，黎曼给出这里的s值实部为1/2的结果，即分布在一条直线上，这几乎等同于告诉大家，质数随机分布在直线1/2上。

黎曼猜想被证明的重大意义

如大家所知，随机分布因无规律可循，所以也是最为安全。因此，现阶段的密码学系统，包括新兴的区块链底层架构，都是基于质数分布的随机性来构建和设计的，以确保一定的安全性。

除了对数论有着非常大的影响，物理、机械、信号等与频率（复分析）有着密切联系的应用领域，都将会或多或少的受到这一证明过程的影响和启发。

某种程度上，黎曼做的事情就是给后辈们指引一条极具意义的方向，而每一种证明思路都将进一步推进这一理论的发展，以及对其他学科的渗透。

附上网络流出的 Atiyah论文图，仅供参考：

注：图片来源于网络