俗话说得好，赌一赌单车变摩托，搏一搏摩托变路虎。谁都想要单车变路虎，但问题是怎么做？

很简单，抛硬币就可以实现。

比如隔壁老王来找你抛硬币。

正面，他给你一块钱，反面，你给他一块钱。

扔硬币这种事情，正反面概率各是50%，但是一块钱一块钱地赌实在是太慢了，万一你一开始输了10局，你还得赢10局才能扳回来。人生有多少个10局可以重来？

为了能确保战胜老王赚到钱，你提出一个要求，如果你加注他也必须要加注，也就是说如果你下注2块，那么，正面他给你2块钱，反面你给他2块钱。

这很公平，老王答应了。

为什么你的策略能保证战胜老王？

因为一旦输了，下一把你就翻倍加注，比如，第一把输了，第二把就下注2块，又输了，就下注4块，以此类推，直到你赢了一把，就能完全弥补，因此只要能让你一直赌下去，你一定是赢钱的。这种激进的操作方法有种学术上的称呼。

等价鞅策略（Martingale strategy）

Martingale据说是法国的一个小镇，居民非常精打细算，今天花过一块钱能推算出下个星期花几块钱。某位法国数学家对小镇人民的艰苦朴素精神印象深刻，干脆将自己思考出来的理论用Martingale来命名。后来发展为知名的鞅定价理论。（Martingale pricing theory）

至于为什么翻译成鞅，据说martingale这个单词在法语中意思就是马的缰绳……

然而明眼人一看就发现，要实现等价鞅策略必须满足两个条件，首先你得有足够多的本金，其次是你有无限的对赌次数。在现实生活中这种设定一看就行不通，如果你有隔壁王首富那样的财力做什么不好，去和人家1块钱赌抛硬币？

因此，在此基础上诞生了反等价鞅策略。

所谓反等价鞅策略则是为了能无限地参与赌局，而不要越亏越加码。

操作也很简单，每次你都拿出全额本金中的固定比例参与赌局，让自己的剩余本金永远不等于零。

问题是，如何确定出资的比例，使你在赌局中既不会下注太少玩得不爽，又不至于一把压多，输到心颤。

凯利公式（Kelly formula）就此诞生。

凯利公式的目的很简单，就是帮助你确定究竟下注的出资比例f是多少对你最有利。

从数学推导上说，假设你一开始有A元，每次出资比例是f，那么你第一次下注就是A*f 元

如果第一把你赢了，你的本金就增加了A*b*f 元（b是赔率＝期望收益÷可能亏损，在抛硬币中是2:1）

如果第一把你输了你的本金就减少了A*f 元。

如果老王抛硬币抛了T次，你赢了W次，输了L次，即T=W+L

最终可以推导出抛完T次后你手里还有多少钱。

A（T）=A*（1+bf）^W*（1-f）^L

求出f让你的A（T）有最大值，f就是你的最佳出资比例。

附上推导过程，嫌麻烦可以略过。

f=（p（b+1）-1）/b

其中

f 就是最佳出资比例；

b 是你赌局的赔率；

p 是这一把的成功率；

人尽皆知的投资家巴菲特更是进一步简化公式，另赔率b=1 ，也就是使你的期望收益和可能亏损完全相同，震荡幅度对称。

巴菲特版凯利公式出奇的简单：

f =2p-1

比如在你和隔壁老王的抛硬币游戏中，赔率是2:1,那就不能用巴菲特版的公式了，只有根据原版公式进行计算。

而扔硬币这种事情的概率各是50%。

数据代入凯利公式，得到结论是25%的资金投入比例。

也就是说如果和老王赌抛硬币，假设你本金有100，第一把就该下注25！如果第一把输了，就下注75块的四分之一。

那么在实战中凯利公式的效果如何？

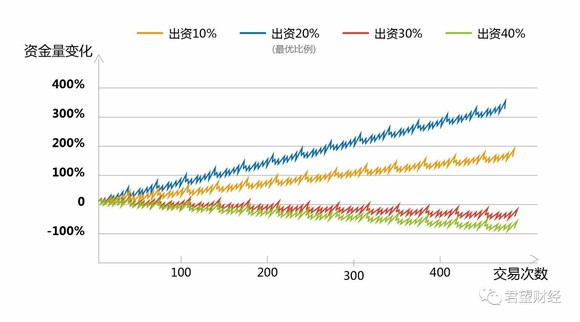
按照相同的仓位比例进行下注模拟交易，在大量交易次数后的结果就如上图所示。仓位比例孰优孰劣一看便知。

凯利公式的两个变量：赔率和成功率。

f =p+ (p-1)/b

根据小学的四则运算，我们不难看出，假设p不变，赔率b越大，出资比例f越大。

那么，成功率p较小而赔率b较大的情况和p较大b较小的情况相比较，会得出什么样的结论呢？

结论是，成功率p较大b较小的情况更适合追加出资比例。

结合实际的A股市场，凯利公式表达的含义就是宁可选择上涨概率大，上涨幅度有限的股票建仓，也尽量减少上涨概率小，却有可能一夜暴涨的股票建仓。

甚至从另一种角度来说，假设你看中了一支个股准备建仓，即，你的f是大于零的，并且你预估了一个自己能接受的盈利率和止损率，也就是赔率b，根据凯利公式你可以倒推成功率p。（在A股市场中p就代表一支股票上涨到期望收益价位的概率）

言下之意，如果你对上涨的概率判断把握是高于p的，你可以建仓并且增加仓位，反之则减仓甚至抛售股票。

听上去，凯利公式确实是很有帮助，根据凯利公式计算的结果，似乎是能够帮助自己“逢赌必赢，炒股必赚。”

那么凯利公式的运用有缺陷吗？

当然，答案非常明显，并且体现在了上述的数学公式推导中。

凯利公式成立并且使你获得最大收益的前提是T趋近于无穷大。

也就是说你能无限次地进行交割操作，时时刻刻+1s，永生一般地在时刻炒股，因为只有这样，你的上涨概率p才能用极限求出一个确定值。

而我们知道，现实中，谁都不可能有无限次的交易次数T。

那么该怎么办？如果行情低迷，我们真的就只是极小比例出资，闲置大量资产吗？

并不是。

这时候我们可以结合等价鞅思想来进行风险控制。

等价鞅策略的思想通俗地说是越亏越加码，保证多次交易自己是盈利的，只不过前提是你有很多本金。

那如果反向思考，既然本金是有限的，保证多次交易自己的亏损是有上限的，也就是越赚越减仓。利用等价鞅思想帮助自己风险控制。

比如你总资产100万元，计算出投资比例f =10%也就是10万，你设定的风险上限也就是期望亏损是20%的可能亏损。

假设你一开始亏到了8万，那么继续投入10万，建仓金额总计18万，如果赚到了20万，那就提出10万，继续从10万元重新开始。

如果18万后你的股票继续跌，到16万的风险上限后增加20万，建仓金额共计36万。以此类推，如果你持续地判断错误，持续地加仓都跌，那么总资产剩80万的时候止损。

这样做的意义是什么？

在你10万亏了20％的时候，从18万回到20万的回报率只需要11.1%

当你20万亏了20％的时候，从36万回到40万的回报率只需要11.1%

对回报率的要求下降后，调整了自己的期望收益，这时候再根据上涨概率p再次进行选择。

通俗地说就是用等价鞅的思想亏损加仓，赚钱减仓，确保在每一次交易时，自己都处于优势状态。

既不会交易了几次就达到止损边界，也不会因为上涨概率p难以判断而不敢建仓。

当然，公式的运用在于数值的可确定性。所谓的必赢局面，也必须建立在数值确定的基础上。

对于扑朔迷离的中国A股市场，几乎只有10%的日波动浮动上限是可确定的数值。

各路资金的行踪也是诡变莫测。

即使是牛顿这样的物理学家也只能感叹：我能计算出天体运行的轨迹，却难以预料到人性的疯狂。